| Calendar of the Ancient Kazakh Nomads | |
|---|---|
| by Peter J. Meyer | |
Most of the text in this article is taken from
the author's page on the Kazakh Nomad Calendar software.
For thousands of years ethnic Kazakhs roamed the steppes of what is now Kazakhstan, the 9th largest country in the world. They were nomads, who lived by grazing sheep and goats. Their mode of transport was by horse and camel, and they lived in moveable round tents call yurts (at the apex of which was a hole through which the Moon and stars could be observed). The language of the nomads had no written form, but nevertheless they managed to develop a remarkable lunisolar calendar based on the relation in the sky between the Moon and the Pleiades star cluster, of which the central and brightest star is called "Alcyone".
In comparison with the Chinese lunisolar calendar, the principles underlying the Kazakh Nomad calendar are quite simple. They were stated by Kaldarkhan Aliseituly Kambar, a descendant of the ancient Kazakh nomads, in an article[1] about the Maya Calendar where he says:
The star calendar, based on the sidereal cycle of the Moon, in practice is used very seldom. It is also the most ancient calendar. Such calendars under the name togys (from kazakh togysu meaning “to intersect’ [occultation]) were used by Kazakhs. The beginning of months coincides with the moment when the Moon passes the Pleiades and the names of months correlate with lunar phases. As the difference between the synodic and sidereal cycles of the Moon is about 2 days, each subsequent meeting of the Pleiades and the Moon occurs on a lunar phase that is 2 days earlier than the previous lunar phase.
Stated more precisely, a month in the Kazakh Nomad Calendar begins on the nychthemeron (the midnight-to-midnight local time period for the Kazakh nomads) during which the Moon (appearing to travel in the sky from east to west) attains the same right ascension (to use a modern astronomical term) as the (stationary) Pleiades (or, for exactness, the central star Alcyone). If, at this time, they have the same or similar declination, so that the Moon appears to cover the Pleiades, then we have what is called an "occultation". There are years-long periods[2] when an occultation occurs each month, followed by years-long periods when there is no occultation (but the Moon still passes the Pleiades, above or below).
Astute readers will now ask: Since the nomads (presumably) did not have the modern astronomical concepts of celestial sphere and right ascension, how did they know when the Moon attained the same right ascension as the Pleiades? Especially because this event does not occur when, from the point of view of an observer on the ground, the Moon is exactly above or below the Pleiades.
The nomads understood that (in modern language) the Moon and the Pleiades had the same right ascension when the line joining them could be extended northward to reach the pole star (our "Polaris", which the nomads called the "Iron Stake"). Below is a screenshot from the Stellarium planetarium program (the blue lines mark right ascension and declination) showing the view of the night sky from Almaty at 20:50 on October 26, 2018, when the right ascension of the Moon is the same as that of the Pleiades, namely, 3h46m58s. Although the Pleiades is above and to the left of the Moon, as observed from the ground (the horizon is shown at the bottom), the Pleiades can be seen to lie on an imaginary line joining the Moon and Polaris.
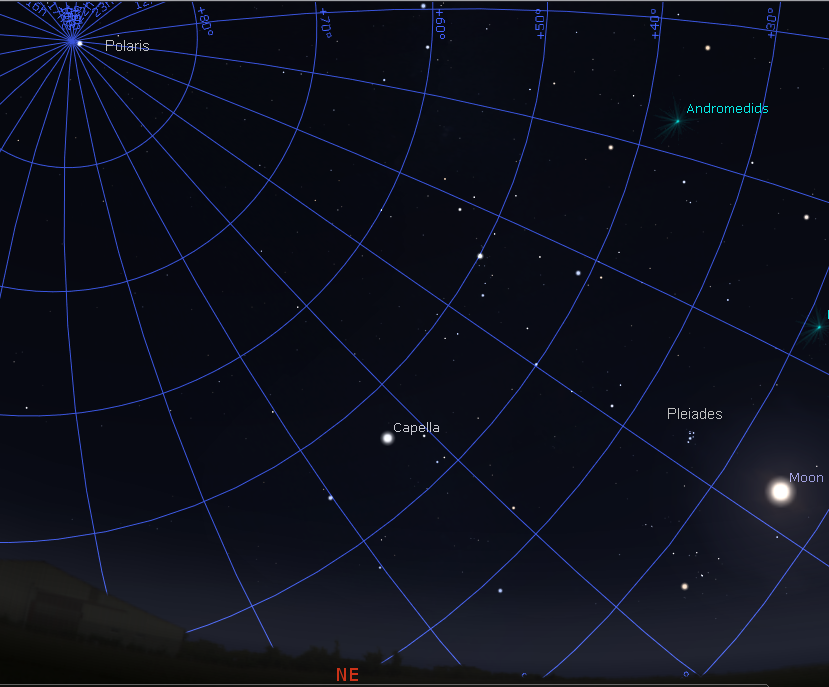
The time of the passing of the Pleiades by the Moon (marking the first day of the month) is less easily determined when the event occurs during daylight, when the Pleiades is not visible. However, as the old month drew to a close, the nomads observed the Pleiades and the Moon at night, when both were visible, and if in the early hours of some day (nychthemeron) the Moon had not yet reached the Pleiades, and in the late hours (before midnight) it had passed the Pleiades then, although the exact alignment (that is, equal right ascension) occurred during the daylight hours, these two observations were sufficient to establish that this nychthemeron was the first day of the month.
Now, of course, the time of the event can be calculated exactly (by simulation of the motion of the Moon), thus providing a firm astronomical underpinning to the Nomad Calendar.
Because the sidereal period of the Moon — the time it takes to return to the same position (more exactly, same right ascension) in the sky, such as the position of the Pleiades — is approximately 27.3 days, such a sidereal month, when measured in days, always has either 27 or 28 days.
The Kazakh nomads developed their calendar for meteorological and agricultural purposes. Thus they needed a seasonal calendar. They managed to do this by segmenting the sequence of sidereal months into seasonal years, where a year begins on the day (nychthemeron) at which a crescent moon first becomes visible following a dark moon. (A dark moon occurs when the Moon is exactly between the Earth and the Sun and is thus invisible.) It turns out that a year in the Kazakh Nomad Calendar always has either 13 or 14 (sidereal) months, a 13-month year (almost) always has either 355 or 356 days, and a 14-month year (almost) always has either 382 or 383 days.
Like the Chinese, the Kazakh nomads named years by using a cycle of 12 animal names. In order they are "Mouse", "Cow", "Leopard", "Hare", "Wolf", "Snake", "Horse", "Sheep", "Monkey", "Hen", "Dog" and "Boar". The sequence of years was thus divided into 12-year periods
The months were not numbered in the traditional nomad calendar, instead they were named as follows:
| Traditional Nomad Month Names | ||||
| Month number | In a year of 13 months | In a year of 14 months | ||
| 1 | 1 togys | 1 togys | ||
| 2 | 25 togys | 27 togys | ||
| 3 | 23 togys | 25 togys | ||
| 4 | 21 togys | 23 togys | ||
| 5 | 19 togys | 21 togys | ||
| 6 | 17 togys | 19 togys | ||
| 7 | 15 togys | 17 togys | ||
| 8 | 13 togys | 15 togys | ||
| 9 | 11 togys | 13 togys | ||
| 10 | 9 togys | 11 togys | ||
| 11 | 7 togys | 9 togys | ||
| 12 | 5 togys | 7 togys | ||
| 13 | 3 togys | 5 togys | ||
| 14 | 3 togys | |||
The "togys" number is (very) approximately the number of days of the age of the Moon on the 1st day of the month. The year begins with the month whose 1st day occurs when the Moon passes the Pleiades immediately after a dark moon (when the crescent Moon first becomes visible), so at that time the age of the Moon is approximately 1 day. When the 2nd month begins, approximately 27 days later, the Moon has not yet completed the lunation (namely, the lunation which began one month earlier), and its age is something like 27 days. With each successive month the age of the Moon decreases by about 2 days, and the month names decrease to "3 togys", the name of the final month of the year.
It is uncertain whether the Kazakh nomads distinguished between one 12-year cycle and those preceding and succeeding it. In order that dates in the Nomad calendar should designate days unambiguously, it is necessary to distinguish those cycles.
This could be done by a system of numbered cycles each containing a certain number of subcycles. It is, however, simpler to number the cycles sequentially from a chosen base year, with that year being designated a Mouse year. This allows us to write a Nomad Calendar date in the short form:
{cycle-number}-{animal name of year}-{month}-{day number}
where {month} is either a numeral or the name of a moon phase (in the style of the nomads, as explained above).
If we choose -3680 (that is, 3681 BCE) as the base year then Cycle #1 consists of the years -3680 through -3699 (that is, 3681 BCE through 3700 BCE). If the cycles are so numbered, then the 12-year period from 2008 CE through 2019 CE is Cycle #474.
A second extension could be made, namely, a 7-day week cycle similar to the European 7-day cycle ("Monday", etc.) but with different names ("Arcturus", etc.). The reason for this is explained in the next section.Each month in the Nomad Calendar has either 27 or 28 days. Thus, unlike months in the Gregorian Calendar, every month can be partitioned into three 7-day weeks plus a final week of either 6 or 7 days. This makes scheduling events much easier than with the Gregorian Calendar, whose months consist mostly of four 7-day weeks plus 2 or 3 days more. Moreover, the first day of a Gregorian month can have any weekday name, and for a particular month the weekday name of the first day of the month varies from year to year. It is thus difficult to select and announce dates for events (months or even years in advance) which should begin on a particular day of the week.
As in the Gregorian Calendar, the first day of the month in the Nomad Calendar does not always fall on the same day of the European week. Regularity, however, can be obtained simply by using a different system of seven weekday names, names of stars which are among the brightest in the night sky, namely, "Arcturus", "Betelgeuse", "Canopus", "Deneb", "Elnath", "Fomalhaut" (these run from "A" to "F") plus "Sirius", as shown below. The name of a particular day in a Nomad month is then easy to remember, since the sequence is the same for each of the four weeks. For example, "Canopus" is the name of the 3rd day in each week, thus the name of Days 3, 10, 17 and 24. A "Sirius" day always occurs on Days 7, 14 and 21, and on Day 28 in a month with 28 days. Thus for scheduling purposes (e.g., the semesters, courses and lectures at an educational institution) this calendar is vastly superior to the Gregorian Calendar.
For use in Western countries the nomad month name can be replaced by the number of the month, so dates would be of the form:
{cycle-number}-{animal name of year}-{month number}-{day number}
as in "475-Mouse-2-24 KN" (= "2020-06-14 GC"). Replacing the animal year name by its number would give the purely numerical (and computer-friendly) form of the date, "475-01-02-24 KN".
A full description of this software (and a download link) is available at the author's website[4].
In principle, for each Gregorian date from 3681 BCE onward there is a unique corresponding date in the Nomad Calendar. However, the earliest Gregorian date that can be converted using this software is April 16, 1600 (= 440-Mouse-1-1 KN), and the latest is December 24, 2099 (= 481-Sheep-8-25 KN). The reason for this limitation is that the calculation of the exact time of the Moon's overtaking of the Pleiades requires the determination of the lunar longitude and latitude at a specific time (to within 1 minute). Or rather, an estimate of these values, because the position of the Moon is increasingly uncertain prior to 1600 CE and after 2100 CE. As we move further into the 21st Century (and astronomical research continues) the "latest date" will probably move forward and remain well ahead ahead of the current date.
[1] Kambar, K. A., NEW LOOK AT THE MODERN CODIFICATION OF THE MAYAN CALENDAR
www.hermetic.ch/cal_stud/maya/Mayan_Calendar_New_Look.pdf
[2] Können, G. P. & Meeus, J.: Occultation series of five stars
adsabs.harvard.edu/full/1972JBAA...82..431K
[3] Peter J. Meyer, Julian Day Numbers
www.hermetic.ch/cal_stud/jdn.htm
[4] Peter J. Meyer, The Kazakh Nomad Calendar Software
https://www.hermetic.ch/knc/knc.htm