A Little Number Theory
by Peter Meyer

In Volume 3 Number 3 of Apple Gram Greg Enos poses a problem involving 1000 doors and 1000 men. Initially all doors are closed; each man in turn then opens or closes doors as follows: The kth man opens/closes the kth door and each subsequent kth door. So, e.g., after the first two men have done their thing, the third man opens/closes the 3rd, 6th, 9th, ..., 999th doors.

Query: After all men are through, which doors are open?

Answer: Door n is open if and only if n is a perfect square.

The problem raised, to which I will here provide an answer is: Why?

The reasoning below is based on elementary algebra and number theory. In what follows "iff" stands for "if and only if".

Consider door n. This is opened/closed by the kth man iff n is divisible by k (as a little reflection will reveal). k may be 1 or n (the first door is opened by the first man, and the last door is opened or closed by the last man).

All doors are initially closed, so after all the men have done their thing door n will be open iff it was opened/closed an odd number of times iff n has an odd number of divisors (including 1 and n).

By a well-known number theorem, an integer > 1 may be expressed uniquely as a product of primes > 1, thus: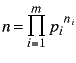

Clearly the number of divisors of n (including 1 and n) is: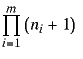

This is odd iff ni + 1 is odd for all i ( 1 <= i <= m) iff ni is even for all i.

Thus the number of divisors of n is odd iff n may be expressed as a product of primes thus: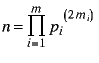

Since this equals 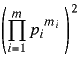, a perfect square, we have that the number of divisors of n (including 1 and n) is odd iff n is a perfect square. This completes the proof.

This article has been published only once before,
in Apple Gram, the magazine of the Apple Corps of Dallas.
It appeared in the August 1981 issue on pages 21-22.

Mathematical Software Hermetic Systems Home Page