The proof is in three parts.
| Lemma 1: |
Proof: The number of ways of throwing n dice with m faces is the sum of the number of ways of throwing n m's plus the number of ways of throwing n-1 m's and 1 non-m plus the number of ways of throwing n-2 m's and 2 non-m's ... plus the number of ways of throwing 0 m's and n nom-m's. Clearly this is equal to the sum of the number of ways of throwing 0 dice with m-1 faces plus the number of ways of throwing 1 die with m-1 faces plus the number of ways of throwing 2 dice with m-1 faces ... plus the number of ways of throwing n dice with m-1 faces. This is N(0,m-1) + N(1,m-1) + N(2,m-1) + ... + N(n,m-1), which proves the lemma.
| Lemma 2: |
| Proof: By Lemma 1 we have that |
| = | 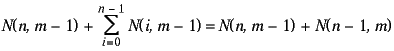 |
We now state the theorem in the following form and prove it by induction on k:
Theorem: For all k ≥ 2, if n ≥ 1 and m ≥ 1 are such that n + m = k then
N(n,m) = ( n + m - 1)! / ( n! * ( m - 1 )! )
Proof: Consider k = 2. Suppose n + m = k, then n = 1 and m = 1. N(1,1) = 1 and
( 1 + 1 - 1)! / ( 1! * ( 1 - 1 )! ) = 1. Thus the theorem is true for k = 2.
Suppose the theorem is true for k - 1, then we shall show it is true for k.
Suppose n and m are such that n + m = k. By Lemma 2, N(n,m) = N(n,m-1) + N(n-1,m).
Since n + m - 1 = k - 1 and n - 1 + m = k - 1 we have that
N(n,m-1) = ( n + m - 2 )! / ( n! * ( m - 2 )! ) and
N(n-1,m) = ( n - 1 + m - 1 )! / ( ( n - 1 )! * ( m - 1 )! ).
Thus N(n,m-1) + N(n-1,m)
= (( n + m - 2)! * ( m - 1 )) / ( n! * ( m - 1)! )
+ ( n + m - 2 )! * n ) / ( n! * ( m - 1 )! )
= ( n + m - 2)! * ( n + m -1 ) / ( n! * ( m - 1 )! )
= ( n + m - 1)! / ( n! * ( m - 1)! )
which shows the theorem to be true for k. This completes the proof.
| Mathematical Software | |
| Index | Home Page |