The Value of Tau

The number eponymous with the Greek letter tau is defined as

To find the exact value of (at least to a certain number of decimal places) we can take the easy way and write a short C program, TAU.C. The output of the program is:

This program calculates tau to 16 decimal places thus:
tau = sqrt(1 + sqrt(2 + sqrt(3 + sqrt(4 + ... + sqrt(22)))...)))
1.5537739740300374 = sqrt(1+sqrt(2))
1.7122650649295326 = sqrt(1+sqrt(2+sqrt(3)))
1.7487627132551438 = sqrt(1+sqrt(2+sqrt(3+sqrt(4))))
1.7562384875823431 = sqrt(1+sqrt(2+sqrt(3+sqrt(4+sqrt(5)))))
1.7576412350415822 = sqrt(1+sqrt(2+sqrt(3+sqrt(4+sqrt(5+sqrt(6))))))
1.7578856460964372 = sqrt(1+sqrt(2+sqrt(3+sqrt(4+sqrt(5+sqrt(6+sqrt(7)))))))
1.7579255575682606 = sqrt(1+sqrt(2+sqrt(3+sqrt(4+sqrt(5+...+sqrt(8))))))))
1.7579317105145658 = sqrt(1+sqrt(2+sqrt(3+sqrt(4+sqrt(5+...+sqrt(9)))))))))
1.7579326113938309 = sqrt(1+sqrt(2+sqrt(3+sqrt(4+sqrt(5+...+sqrt(10))))))))))
1.7579327372820677 = sqrt(1+sqrt(2+sqrt(3+sqrt(4+sqrt(5+...+sqrt(11)))))))))))
1.7579327541406276 = sqrt(1+sqrt(2+sqrt(3+sqrt(4+sqrt(5+...+sqrt(12))))))))))))
1.7579327563117013 = sqrt(1+sqrt(2+sqrt(3+sqrt(4+...+sqrt(13)))))))))))))
1.7579327565813685 = sqrt(1+sqrt(2+sqrt(3+sqrt(4+...+sqrt(14))))))))))))))
1.7579327566137564 = sqrt(1+sqrt(2+sqrt(3+sqrt(4+...+sqrt(15)))))))))))))))
1.7579327566175260 = sqrt(1+sqrt(2+sqrt(3+sqrt(4+...+sqrt(16))))))))))))))))
1.7579327566179521 = sqrt(1+sqrt(2+sqrt(3+sqrt(4+...+sqrt(17)))))))))))))))))
1.7579327566179990 = sqrt(1+sqrt(2+sqrt(3+sqrt(4+...+sqrt(18))))))))))))))))))
1.7579327566180039 = sqrt(1+sqrt(2+sqrt(3+sqrt(4+...+sqrt(19)))))))))))))))))))
1.7579327566180045 = sqrt(1+sqrt(2+sqrt(3+...+sqrt(20))))))))))))))))))))
1.7579327566180045 = sqrt(1+sqrt(2+sqrt(3+...+sqrt(21)))))))))))))))))))))

Thus even though is defined by an expression which involves the unlimited addition of increasingly large integers it is nevertheless a finite quantity, namely, 1.7579327566180045 (to 16 decimal places) — another mathematical oddity.

---

Consider now the series of 's, defined (for n = 0, 1, 2, 3, ...) as follows:

We can adapt TAU.C to give TAU2.C, which calculates the series of 's, and gives the following results:

This program calculates the series of tau(n), where
tau(n) = sqrt(1^n + sqrt(2^n + sqrt(3^n + sqrt(4^n + ..,))))

tau(0)  =  1.6180339887498949
tau(1)  =  1.7579327566180045   diff = 0.139899
tau(2)  =  1.9426554227639874   diff = 0.184723
tau(3)  =  2.1767885971334420   diff = 0.234133
tau(4)  =  2.4674045317177931   diff = 0.290616
tau(5)  =  2.8234815128342032   diff = 0.356077
tau(6)  =  3.2559047054957255   diff = 0.432423
tau(7)  =  3.7777293307595237   diff = 0.521825
tau(8)  =  4.4045817066589290   diff = 0.626852
tau(9)  =  5.1551576862917514   diff = 0.750576
tau(10) =  6.0518133295215266   diff = 0.896656
tau(11) =  7.1212594166022409   diff = 1.069446
tau(12) =  8.3953802511653048   diff = 1.274121
tau(13) =  9.9122027969110444   diff = 1.516823
tau(14) = 11.7170469518366320   diff = 1.804844

Thus we see that:

1. Taking powers of 2, 3, etc., does not cause the series of partial sums to become infinite;
   each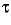 (n) is a particular real number.
2. The series of sums, i.e. the series of 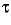(n)'s, does not tend to a limit;
   for any real number r there is some n such that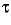 (n) > r.

---

Finally we may note from the case of (0) that

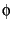which is 1.618033989..., also known as , the "golden mean" — yet another mathematical oddity.

Actually we can prove this equality quite easily:   , so , so solving this quadratic equation for (0) gives .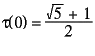

The Greek Alphabet	Mathematical Software
Hermetic Systems Home Page