| Cryptosystem ME6: Statistical Tests |
|
Introduction Statistical Tests Single-bit Change Common Key Cryptotext XOR |
For example, suppose a sequence of bytes was such that twice as many 1 bits occurred as 0 bits (among the bits making up the bytes). In this case, when asked to guess the next byte in the sequence, you are likely to be right more often than not if you choose a byte with more 1 bits than 0 bits. Thus a truly random sequence of bytes should have about as many 0 bits as 1 bits (though it is not likely to have exactly the same number of each).
Ciphertext produced by Cryptosystem ME6 has been subjected to a number of statistical tests in an attempt to find some regularity that would distinguish it from randomly generated bytes. No such regularity has been found. The tests applied to ME-ciphertext are described below, with sample results.
Cryptosystem ME6 compresses the plaintext when possible (which is usually the case). This compression eliminates most regularities in the plaintext, and thus works against the purpose of this test, which is to see whether the encryption process itself removes all pattern. Thus in this test a version of the Cryptosystem ME6 software was used which does not compress the plaintext (and which also does not interchange the two halves of each block, as normally occurs according to the description of the encryption process).
For this test (and for the other tests described below) three files were created, each consisting only of repetitions of the 32-byte sequence

Each file was encrypted using the 16-byte key PPPPPPPPPPPPPPPP (the hexadecimal representation of P is 50 and its binary representation is 01010000). The randomness measures for the plaintext files and for the encrypted files (with and without compression) are given below.
The randomness measures were as follows:
The plaintext:
File Size in bytes Randomness
4k1.tst 4,096 0.182
64k1.tst 65,536 0.134
1024k1.tst 1,048,832 0.106
The ciphertext (without compression):
File Size in bytes Randomness
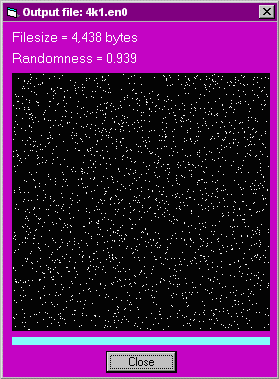
4k1.en0 4,439 0.939
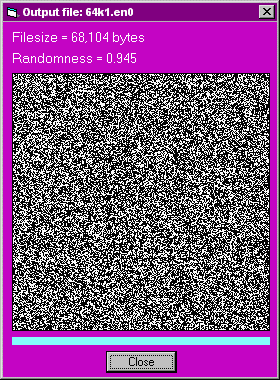
64k1.en0 68,105 0.945
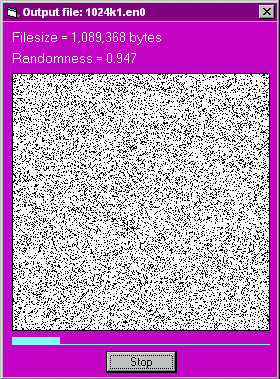
1024k1.en0 1,089,368 0.947
The ciphertext (with compression):
File Size in bytes Randomness
4k1.en1 994 0.952
64k1.en1 10,046 0.952
1024k1.en1 161,387 0.940
These randomness values show that the ciphertext appears as if composed of randomly generated bytes (whether or not compression is used).
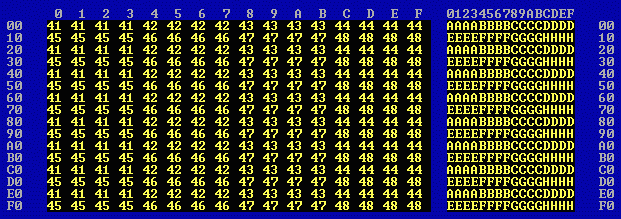
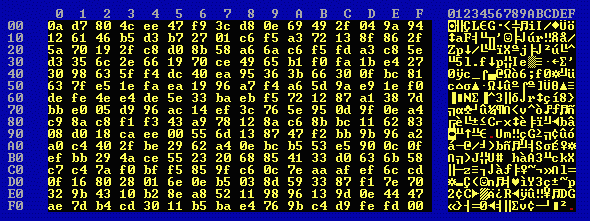
The first 256 bytes of 4k1.en0 look like this:
The graphical displays of randomness for the three ciphertext files (without compression) are:
|
|
 |
One can count the frequency with which byte values occur in the three ciphertext files. The 20 most-frequent byte values are as follows:
File 4k1.en0 contains 4439 bytes and 256 different byte values.
Rank Byte Frequency ASCII value
1 126 = 0x7E 30 ~
2 164 = 0xA4 30
3 57 = 0x39 27 9
4 35 = 0x23 26 #
5 128 = 0x80 26
6 221 = 0xDD 26
7 135 = 0x87 25
8 171 = 0xAB 25
9 69 = 0x45 24 E
10 76 = 0x4C 24 L
11 187 = 0xBB 24
12 46 = 0x2E 23 .
13 48 = 0x30 23 0
14 54 = 0x36 23 6
15 77 = 0x4D 23 M
16 84 = 0x54 23 T
17 124 = 0x7C 23 |
18 184 = 0xB8 23
19 193 = 0xC1 23
20 210 = 0xD2 23
File 64k1.en0 contains 68105 bytes and 256 different byte values.
Rank Byte Frequency ASCII value
1 5 = 0x05 327
2 36 = 0x24 312 $
3 99 = 0x63 307 c
4 182 = 0xB6 302
5 75 = 0x4B 301 K
6 22 = 0x16 299
7 250 = 0xFA 299
8 0 = 0x00 298 null
9 8 = 0x08 298
10 143 = 0x8F 298
11 188 = 0xBC 298
12 236 = 0xEC 298
13 120 = 0x78 296 x
14 145 = 0x91 294
15 247 = 0xF7 294
16 28 = 0x1C 293
17 53 = 0x35 293 5
18 187 = 0xBB 293
19 135 = 0x87 292
20 195 = 0xC3 292
File 1024k1.en0 contains 1089368 bytes and 256 different byte values.
Rank Byte Frequency ASCII value
1 203 = 0xCB 4395
2 236 = 0xEC 4394
3 12 = 0x0C 4393 formfeed
4 174 = 0xAE 4388
5 193 = 0xC1 4383
6 108 = 0x6C 4380 l
7 94 = 0x5E 4376 ^
8 10 = 0x0A 4373 linefeed
9 206 = 0xCE 4367
10 214 = 0xD6 4365
11 99 = 0x63 4362 c
12 250 = 0xFA 4362
13 209 = 0xD1 4359
14 29 = 0x1D 4354
15 91 = 0x5B 4354 [
16 146 = 0x92 4354
17 102 = 0x66 4351 f
18 151 = 0x97 4348
19 160 = 0xA0 4347
20 21 = 0x15 4345The byte values are thus distributed uniformly, which is what we would expect for ciphertext in which the bytes appear to be random.
The 4k1.en0 and 64k1.en0 files were analysed as to their bit counts (1024k1.en0 was too large for the analysis program), not only for total bit counts but also for bit counts for the 8 positions within a byte. The results were:
4k1.en0 is 4439 bytes long. Number of zero bits = 17949 Number of one bits = 17563 Difference = 386, 1.087% of total bits bit posn 7 6 5 4 3 2 1 0 0 bits 2276 2252 2210 2240 2207 2265 2253 2246 1 bits 2163 2187 2229 2199 2232 2174 2186 2193 0 - 1 113 65 -19 41 -25 91 67 53 % total 2.546 1.464 -0.428 0.924 -0.563 2.050 1.509 1.194 64k1.en0 is 68105 bytes long. Number of zero bits = 273376 Number of one bits = 271464 Difference = 1912, 0.351% of total bits bit posn 7 6 5 4 3 2 1 0 0 bits 34186 34373 34440 34043 33979 34115 34058 34182 1 bits 33919 33732 33665 34062 34126 33990 34047 33923 0 - 1 267 641 775 -19 -147 125 11 259 % total 0.392 0.941 1.138 -0.028 -0.216 0.184 0.016 0.380
Bytes which are truly randomly generated should have about as many 0 bits as 1 bits. In ME6-ciphertext the number of 0 bits is in fact found to be close to the number of 1 bits, even for the individual bit positions within a byte, so this statistical test, like the others, does not distinguish ME6-ciphertext from randomly generated bytes.
The kappa test is designed to detect repetitions of bytes at specified offsets in a file. Suppose that the elements of the ciphertext are any of the 256 possible bytes (0 through FF in hexadecimal). Consider the ciphertext to be a sequence of bytes (in a row). Now duplicate this sequence and place it beneath the first (with the first byte of the first sequence directly above the first byte of the second sequence). We now have a sequence of pairs of identical bytes. Slide the lower sequence to the right a certain distance, say, 8 places. Then count how many pairs there are in which the bytes are identical. If the sequence of bytes were truly random then we would expect about 1/256 of the pairs to consist of identical bytes, i.e., about 0.39% of them. We may analyse a file, calculating the indices of coincidence (also known as the kappa values) for one or more displacement values (a.k.a offset).
When we run such a program on ordinary English text we obtain values such as the following ("IC" stands for "index of coincidence"):
Offset IC coincidences
1 5.85% 2397 in 40968
2 6.23% 2551 in 40967
3 9.23% 3780 in 40966
4 8.31% 3406 in 40965
5 7.91% 3240 in 40964
6 7.88% 3227 in 40963
7 7.78% 3187 in 40962
8 7.92% 3244 in 40961
9 8.24% 3377 in 40960
10 7.98% 3268 in 40959
11 8.16% 3341 in 40958
12 8.09% 3315 in 40957
13 8.15% 3337 in 40956
14 7.97% 3264 in 40955
15 7.97% 3265 in 40954
16 8.07% 3306 in 40953
17 8.04% 3293 in 40952
18 7.85% 3214 in 40951
Typically only 80 or so different byte values occur in a file of English text. If these byte values occurred randomly then we would expect an index of coincidence for each displacement of about 1/80, i.e. about 1.25%. However, the distribution of characters in English text is not random ("e", "t" and the space character occur most frequently), which is why we obtain the larger IC values shown above.
The kappa test can be useful in breaking a weak cryptosystem. The index of coincidence for the displacement equal to the length of the encryption key will sometimes be significantly higher than the other indices, in which case one can infer the length of the key.
The offset value that is most likely to produce anomalies, in the case of ME6-ciphertext is the key size, in this case 16. The results of running the kappa test on the file 4k1.en0, testing all offset values from 1 through 512, are as follows:
Offset IC coincidences
1 0.41% 18 in 4405
2 0.45% 20 in 4404
3 0.41% 18 in 4403
4 0.39% 17 in 4402
5 0.43% 19 in 4401
6 0.43% 19 in 4400
7 0.43% 19 in 4399
8 0.43% 19 in 4398
9 0.34% 15 in 4397
10 0.30% 13 in 4396
11 0.36% 16 in 4395
12 0.43% 19 in 4394
13 0.39% 17 in 4393
14 0.34% 15 in 4392
15 0.52% 23 in 4391
16 0.25% 11 in 4390
17 0.23% 10 in 4389
18 0.30% 13 in 4388
19 0.27% 12 in 4387
20 0.36% 16 in 4386
...
502 0.33% 13 in 3904
503 0.54% 21 in 3903
504 0.10% 4 in 3902
505 0.38% 15 in 3901
506 0.41% 16 in 3900
507 0.44% 17 in 3899
508 0.38% 15 in 3898
509 0.21% 8 in 3897
510 0.39% 15 in 3896
511 0.49% 19 in 3895
512 0.31% 12 in 3894
Average IC = 0.38%. 256 different byte values occur; kappa-r(256) = 0.39%.
The highest IC values were:
Offset IC coincidences
134 0.61% 26 in 4272
59 0.62% 27 in 4347
344 0.64% 26 in 4062
157 0.64% 27 in 4249
120 0.68% 29 in 4286
105 0.70% 30 in 4301
The results of the kappa test for 64k1.en0, with displacements from 1 through 10,000, are as follows:
Offset IC coincidences
1 0.42% 288 in 68176
2 0.42% 285 in 68175
3 0.42% 286 in 68174
4 0.43% 293 in 68173
5 0.39% 266 in 68172
6 0.44% 299 in 68171
7 0.37% 252 in 68170
8 0.44% 297 in 68169
9 0.39% 265 in 68168
10 0.44% 301 in 68167
11 0.40% 274 in 68166
12 0.37% 251 in 68165
13 0.43% 292 in 68164
14 0.41% 281 in 68163
15 0.42% 286 in 68162
16 0.37% 254 in 68161
17 0.44% 297 in 68160
18 0.35% 236 in 68159
19 0.40% 274 in 68158
20 0.41% 281 in 68157
...
9995 0.37% 215 in 58182
9996 0.38% 223 in 58181
9997 0.38% 220 in 58180
9998 0.41% 237 in 58179
9999 0.39% 228 in 58178
10000 0.38% 219 in 58177
Average IC = 0.39%. 256 different byte values occur; kappa-r(256) = 0.39%.
The highest IC values were:
Offset IC coincidences
2018 0.47% 310 in 66159
34 0.47% 319 in 68143
372 0.47% 322 in 67805
6417 0.48% 294 in 61760
5132 0.48% 304 in 63045
6263 0.49% 303 in 61914Thus the kappa test reveals no regularities in this ciphertext, even though the plaintext consisted solely of repetitions of AAAABBBBCCCCDDDDEEEEFFFFGGGGHHHH and the key was the uniform PPPPPPPPPPPPPPPP.
The absence of any apparent regularities resulting from the encryption method is thus to be expected also in the case where the plaintext is much more diverse (as in normal English text), redundancy is eliminated by compression, and the key is not uniform.
When evaluating an encryption program it is reasonable to ask whether the encryption method used is something as weak as a repeated exclusive-or cipher, in which the bytes of the key are repeatedly XOR'd against those of the plaintext. In a such a cryptosystem each byte of the ciphertext is affected only by the corresponding byte in the key and not by every byte in the key. In this case the system is generally easy to crack (by using the kappa test to determine the length of the key, say n, and then considering the n sets of bytes each consisting of only the bytes encypted by a particular byte in the key).
When an attempt is made to break a cryptosystem this test is likely to be one of the first to be performed, namely, take some known plaintext and encrypt it with slightly different keys and compare the resulting ciphertext to see whether a particular change in the key produces a particular change in the ciphertext. With a strong cipher a change of a single bit in the key will have a cascade effect, producing large changes in the resulting ciphertext.
In this test some plaintext is encrypted, using Cryptosystem ME6, by two keys which differ only in a single byte (and only in a single bit). As stated above, the file 4k1.tst was encrypted (without compression) using the key PPPPPPPPPPPPPPPP to produce the file 4k1.en0 (4406 bytes). 4k1.tst was then encrypted using the key PPPPPPPPPPPPPPPQ, which differs from the first key only in a single bit, to produce the file 4k1.en2 (4355 bytes).
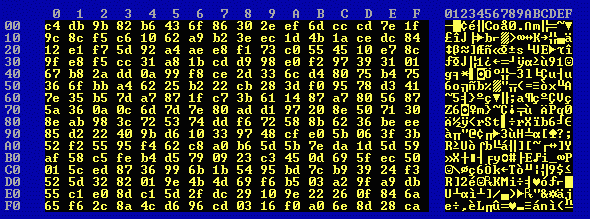
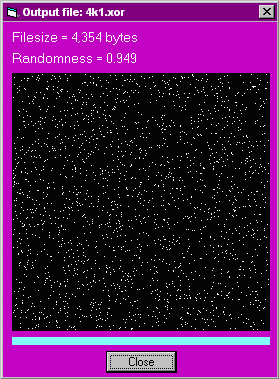
When 4k1.en0 and 4k1.en2 are XORed the result is 4k1.xor, the first 256 bytes of which are:
4k1.xor has a randomness measure of 0.949:
The kappa values show no anomalies (the highest IC with all displacements from 1 through 512 being 0.72%) and the bit count of the 4355 bytes is:
4k1.xor is 4355 bytes long. Number of zero bits = 17537 Number of one bits = 17303 Difference = 234, 0.672% of total bits bit posn 7 6 5 4 3 2 1 0 0 bits 2254 2156 2224 2171 2215 2137 2130 2250 1 bits 2101 2199 2131 2184 2140 2218 2225 2105 0 - 1 153 -43 93 -13 75 -81 -95 145 % total 3.513 -0.987 2.135 -0.299 1.722 -1.860 -2.181 3.330
so these bytes appears to be random and ME6 passes this test (i.e., a single-bit change in the key used to encrypt a file results in ciphertext so different that XORing it with the first ciphertext produces what appears to be random bytes).
(b) Single-bit change in the plaintext
In this test two pieces of plaintext, differing only in a single byte (and in a single bit), were encrypted using the same key.
The two files of plaintext were the file 4k1.tst and a file 4k2.tst (both 4096 bytes in size) differing only in one byte (and in one bit) at the middle of the file, byte 2048, which is an @ (ascii 40) instead of an A (ascii 41).

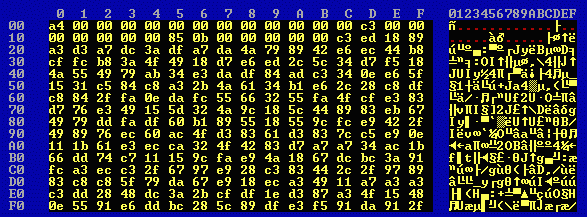
Again the key used for encryption was PPPPPPPPPPPPPPPP. The resulting ciphertext files, 4k1.en0 and 4k2.en0, each 4439 bytes in size, are identical in the first 2218 bytes except for one byte. Then differences begin to appear:

From byte 2720 onwards the two files are completely different:
Thus changing a single bit in the plaintext causes all bytes in all ciphertext sub-blocks (ciphertext segments) following the ciphertext sub-block corresponding to the plaintext sub-block in which it occurs to be different (except for chance coincidences) until the end of the block is reached. And not only different, but so different that the differences appear to be random.
Changing a bit in the plaintext affects only the ciphertext up to the end of the block in which it occurs. A change of one or more bits in one block of plaintext does not affect the ciphertext produced for other blocks of plaintext.
It was shown above that the XOR of two ciphertext files produced with the same key from plaintext files which differ in a single byte consists of garbage from a point in the XOR a few hundred bytes after the position of the byte at which the two plaintext files differ.
In this test we took two quite different plaintext files (of similar length), encrypted them using the same key, formed the XOR and applied the bit count and kappa tests to the XOR. In this test the normal version of Cryptosytem ME6 (i.e., including compression) was used.
The first file was eng1.txt (52,294 bytes) and the second file was eng2.txt (47,829 bytes), each consisting solely of English text. The key was once more unto the breach, the encrypted files being named eng1.enc (32,271 bytes) and eng2.enc (29,198 bytes). These two files were XORed to produce eng.xor (29,198 bytes), whose first 256 bytes are:
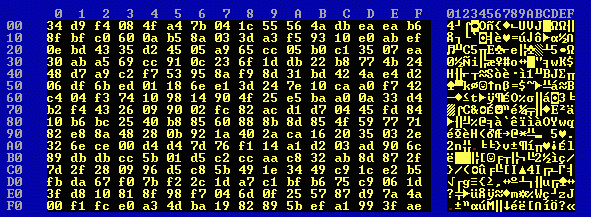
eng.xor has a randomness measure of 0.954:

The bit count test applied to eng.xor produces:
eng.xor is 29198 bytes long. Number of zero bits = 116155 Number of one bits = 117429 Difference = -1274, -0.545% of total bits bit posn 7 6 5 4 3 2 1 0 0 bits 14292 14503 14556 14658 14536 14580 14547 14483 1 bits 14906 14695 14642 14540 14662 14618 14651 14715 0 - 1 -614 -192 -86 118 -126 -38 -104 -232 % total -2.103 -0.658 -0.295 0.404 -0.432 -0.130 -0.356 -0.795Clearly the bit frequencies are uniform.
The kappa test applied to eng.xor, with offsets from 1 to 10,000 produces:
eng.xor is 29198 bytes long.
Offset IC coincidences
1 0.42% 124 in 29197
2 0.42% 123 in 29196
3 0.41% 119 in 29195
4 0.45% 130 in 29194
5 0.36% 104 in 29193
6 0.40% 116 in 29192
7 0.36% 106 in 29191
8 0.41% 120 in 29190
9 0.37% 108 in 29189
10 0.34% 99 in 29188
11 0.43% 125 in 29187
12 0.37% 109 in 29186
13 0.38% 111 in 29185
14 0.44% 129 in 29184
15 0.38% 112 in 29183
16 0.40% 118 in 29182
17 0.50% 147 in 29181
18 0.38% 111 in 29180
19 0.41% 121 in 29179
20 0.39% 114 in 29178
...
9992 0.38% 73 in 19206
9993 0.41% 79 in 19205
9994 0.42% 81 in 19204
9995 0.41% 78 in 19203
9996 0.42% 80 in 19202
9997 0.35% 67 in 19201
9998 0.42% 80 in 19200
9999 0.38% 73 in 19199
10000 0.39% 75 in 19198
Average IC = 0.39%. 256 different byte values occur; kappa-r(256) = 0.39%.
The highest IC values were:
Offset IC coincidences 1536 0.52% 144 in 27662 9819 0.53% 103 in 19379 8806 0.53% 109 in 20392 8738 0.53% 109 in 20460 6254 0.53% 121 in 22944 2423 0.53% 142 in 26775 4291 0.56% 139 in 24907
Thus the kappa test reveals nothing remarkable in the XOR of the two ciphertext files produced using the same key.
| Cryptosystem ME6 | Hermetic Systems Home Page |