Equinoxes, Solstices, and Solar Cross‑Quarter Days

Windows software for calculating the dates and times of vernal and autumnal equinoxes,
summer and winter solstices and the solar cross‑quarter days.

Download of this program has been temporarily suspended

Explanation of the Software

An equinox occurs when the angle formed at the Earth's center between its axis of rotation and the line joining the Earth to the Sun is a right angle. At such a point in the Earth's orbit the length of day and night is equal (or rather, nearly equal, since atmospheric refraction of the Sun's rays affects the actual length). The northern vernal equinox (that is, the vernal equinox in the northern hemisphere) occurs around March 21st of each year, and the northern autumnal equinox occurs around September 21st. In the southern hemisphere these dates are reversed.

A solstice occurs when this angle reaches a maximum or a minimum. At such a point the duration of the day and the night is either longest or shortest. The northern winter solstice occurs around December 21st of each year, and the northern summer solstice occurs around June 21st. In the southern hemisphere these dates are reversed.

The solar cross-quarter days occur midway between the equinoxes and solstices. These are sometimes erroneously called Imbolc, for example (as observed in the northern hemisphere), is midway between the northern winter solstice and the northern spring equinox (also known as the northern vernal equinox), and so-called Beltane is midway between this and the northern summer solstice.

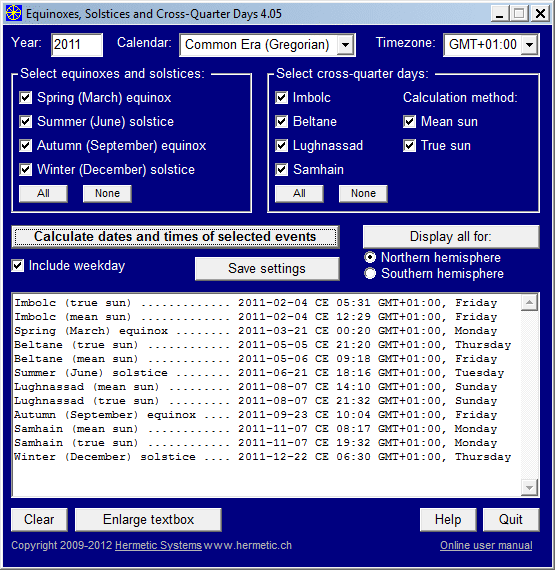
The calculated results are accurate to within a minute or so for years in the vicinity of 2000 CE. ('CE' is the calendar designation for the Common Era Calendar, which is the same as the Gregorian Calendar for years from 1582 onward.) The program gives results for any year in the range 1 CE through 3000 CE, but for years approaching these limits the results are less accurate due to uncertainty regarding the value of delta T. For example, the value of delta T for 1000 CE is about 30 minutes, so assuming a 10% error margin then the times for events at 1000 CE have an error margin of about 3 minutes.

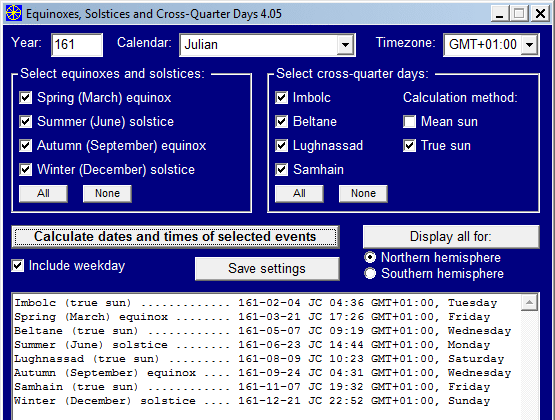
For people interested in dates of these events more than 500 years ago, the dates may be given in the Julian Calendar as well as in the Common Era Calendar. The time of an event is not affected by the choice of calendar, only by the choice of timezone. (Continental U.S. timezones range from GMT‑5 for Eastern Standard Time to GMT‑8 for Pacific Standard Time.)

Mean Sun and True Sun Calculations

An attempt to define the cross‑quarter days more exactly reveals that there are two interpretations, giving rise to two methods of calculation, which give slightly different results. Following the terminology used in connection with the study of the Chinese Calendar, these two methods are named the mean sun method and the true sun method.

The mean sun method assumes (what is not in fact the case) that the Earth moves at a constant speed in a circular orbit around the Sun. Under this assumption the Earth will take the same time to travel from its position (in its orbit) at a solstice (resp. equinox) to its position at the next cross‑quarter point as it takes to travel from that cross‑quarter point to the next equinox (resp. solstice). Then the time of the cross‑quarter point is the time exactly halfway between the times of the solstice (resp. equinox) and the equinox (resp. solstice).

As discovered by Johannes Kepler, however, the orbit of the Earth is an ellipse (although almost a circle) and the speed of the Earth in its orbit around the Sun is not constant. The Sun is at a focus of the ellipse, and thus the distance between the Earth and the Sun varies (though not by much). The Earth travels faster when it is closer to the Sun, and slower when it is more distant. Its speed is greatest when it is closest to the Sun (the point in its orbit known as the perihelion).

The true sun method calculates a cross‑quarter day based on the time at which the Earth reaches that point in its orbit which is spatially (that is, geometrically) exactly midway between its positions at the solstice (or equinox) and the subsequent equinox (or solstice).

A Fuller Explanation of the Difference

The differences between the calculated times for the cross‑quarter days using these two methods will now be illustrated by reference to the times of the cross‑quarter days given above for the year 2006 (for timezone GMT).

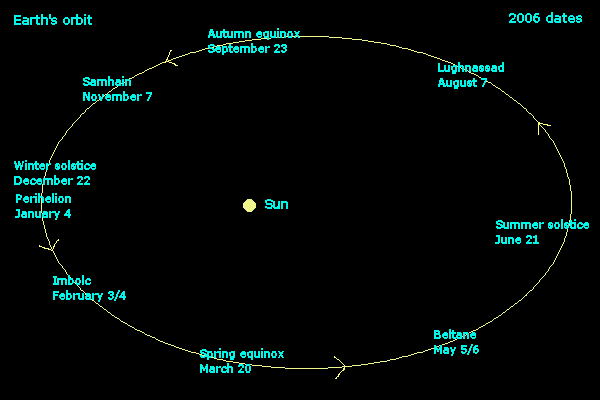
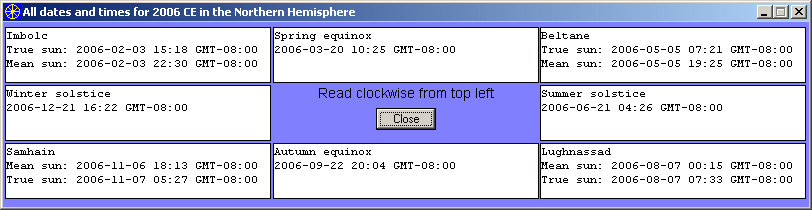
Perihelion currently occurs about January 4 (though it will not always do so), and thus a couple of weeks after the (northern) winter solstice. According to the mean sun method, the Earth reaches the point halfway between the 2005 winter solstice and the 2006 (northern) spring equinox on February 4, 2006 (this is Imbolc). However, the Earth travels faster before reaching this point in its orbit than it does after reaching this point, since the perihelion point occurs between the 2005 winter solstice and the 2006 spring equinox. Thus the Earth actually reaches that point a little earlier than the mean sun calculation suggests, and in fact according to the true sun method the Earth reaches that point not on February 4 but on February 3, about seven hours earlier than the time calculated by the mean sun method.

Now consider Beltane. This occurs between the spring equinox and the summer solstice, and the mean sun method gives a date of May 6. However, the speed of the Earth is still decreasing slightly as it travels between the equinoctial point and the solsticial point, so it is traveling slightly faster before it reaches the cross‑quarter point than after. Thus it arrives at Beltane a little before the time calculated according to the mean sun method. According to the true sun method it arrives on May 5, twelve hours earlier than the time calculated by the mean sun method.

About two weeks after the Earth reaches the summer solstice it begins to speed up in its 6‑month journey to perihelion. The mean sun method calculates that the Earth will reach the point geometrically halfway between the summer solstice and the autumn equinox at 8:15 GMT on August 7. But because the Earth is traveling more slowly before reaching this point than it is after, the Earth takes a little longer to get there than the mean sun method suggests. In fact it arrives at Lughnassad at 15:33 GMT on August 7, about seven hours later than the time calculated by the mean sun method.

The Earth continues to speed up as it travels toward Samhain (between the autumn equinox and the winter solstice) and on toward perihelion. Thus it again arrives there a little later than the mean sun method suggests — 2:13 GMT on November 7. It actually arrives at 13:27 GMT on the same date, thus about eleven hours later than the time calculated by the mean sun method.

From these considerations we can thus see that the true sun method always gives a time slightly earlier than the mean sun method for Imbolc and for Beltane, and slightly later for Lugnassad and for Samhain.

Mean Sun or True Sun Better?

Which is the better method of calculation of the cross‑quarter dates, mean sun or true sun? The mean sun calculation is conceptually simpler: It is the date and time which is exactly halfway between those of the preceding equinox (or solstice) and of the subsequent solstice (or equinox). In contrast, the true sun method gives the times at which the Earth reaches those points in its orbit at which the celestial longitude of the Sun is exactly 45°, 135°, 225° and 315°.

Celestial longitude of the Sun	45°	135°	225°	315°
Cross-quarter day (northern hemisphere)	Beltane	Lughnassad	Samhain	Imbolc
Astrologically	15° Taurus	15° Leo	15° Scorpio	15° Aquarius

Of course, when asking which of two alternatives is "better" one always has to add: "Better for what?" In this case the choice of method (and thus of the calculated dates of the cross‑quarter days) may be a matter of personal preference.

Timezone and Hemisphere Settings

With "Northern Hemisphere" selected, clicking on the "Display All" button shows all dates and times (using both calculation methods) for the selected year, e.g.:

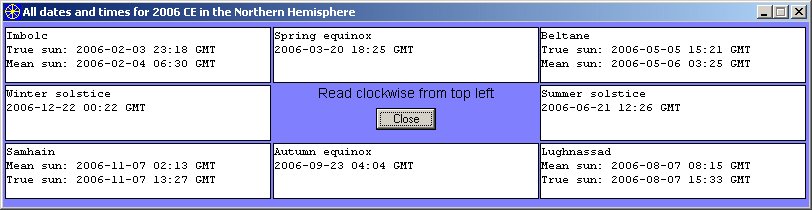
This display is not dependent on the state of the checkboxes on the main screen, but it does depend on the selection of the timezone. When a non‑GMT timezone is selected then the display looks like this (e.g., GMT ‑ 8 for California):

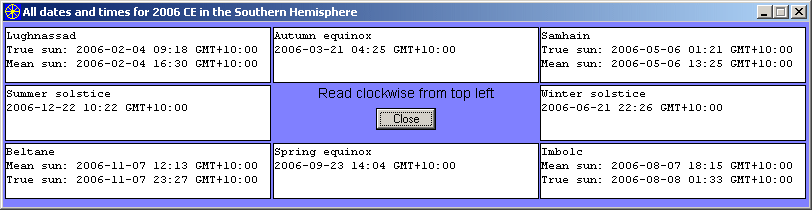
With "Southern Hemisphere" selected, clicking on the "Display All" button shows all dates and times for the selected year, but with the names of the equinoctial, solsticial and cross‑quarter days changed appropriately, e.g.:

A screen resolution of 1024 x 768 or higher is recommended for this software.

An Alternative View of the Dates of Imbolc, etc.

Some schools of thought (e.g., the Lionpath) hold that among the Celts the cross‑quarter days were not celebrated exactly at the dates as calculated above but rather at a full moon or a dark moon nearest to those dates. According to this view the Celts celebrated Imbolc and Samhain at the nearest dark moon, and Beltane and Lughnassad at the nearest full moon.

Applying this to 2006 (and assuming the GMT timezone) we find (using the Lunar Calendars and Eclipse Finder software) that (according to this view) Imbolc is observed on January 29 (not February 3 or 4), Beltane is observed on May 13 (not May 5 or 6), Lughnassad is observed on August 9 (not August 7), and Samhain is observed on November 20 (not November 7).

In the case of that Samhain we note that flanking dark moons occur on October 22 and November 20, and, including the first and last dates, there are 17 days in the period October 22 to November 7 but only 14 days in the period November 7 to November 20 (as we find by using the Easy Date Converter software), so the second dark moon is closer to November 7.

When a full moon occurs during the daylight hours of the day of the calculated date, e.g., Beltane 2006, then a celebration might better be scheduled for the evening of the previous day. For example (again using the Lunar Calendars and Eclipse Finder software) we find that the full moon of May 13, 2006, occurred at 06:51 GMT, so a celebration of Beltane might best have been scheduled for the evening of the previous day, May 12.

Seasons

In Europe and North America there are four seasons in a year: spring, summer, autumn and winter. In some parts of Asia which have a monsoon there are three seasons: cool, hot and wet. By regarding the transitions between these as themselves seasons one can say there are six seasons. Thus the idea of there being exactly four seasons is not valid for the Earth as a whole.

In Europe and North America there is some uncertainty as to when the four seasons begin and end. It is often said that they begin and end at the solstices and equinoxes, so that, e.g., spring begins at the spring equinox (c. March 20) and summer begins at the summer solstice (c. June 21). But because the summer solstice is the longest day of the year (and the day when the Sun reaches its highest point above the horizon), it makes more sense to say that the summer solstice marks the middle of summer, rather than its beginning. If so, summer starts, not three months after the spring equinox, but one and a half months after (c. May 5). From this perspective it makes more sense to say that the four seasons begin and end with the cross‑quarter days, so that spring begins with Imbolc (c. February 4) and ends with Beltane (c. May 5), summer begins with Beltane and ends with Lughnassad (c. August 7), and autumn begins with Lughnassad and ends with Samhain (c. November 7). This seems to have been the custom in earlier times, especially in pagan Europe.

These considerations, however, do not take European and North American climate into account. July and August are generally the hottest months in Europe, so one could say that summer (in the northern hemisphere) is comprised by the three months June‑August; autumn is September‑November, winter is December‑February and spring is March‑May.