Five Cellular Automata |  |
Five Cellular Automata | |
Download of this program has been temporarily suspended
Five Cellular Automata is a program for exploring selected cellular automata. One of these is a generalization of Conway's Game of Life to a multistate cellular automaton (rather than one with just two states). Two of these cellular automata are simulations of chemical or biological processes, and another is related to simulation of physical processes as done in computational physics. The algorithms for each of these cellular automata are described in detail here.
Fullsize screenshots are given in the subsections of this documentation as follows:
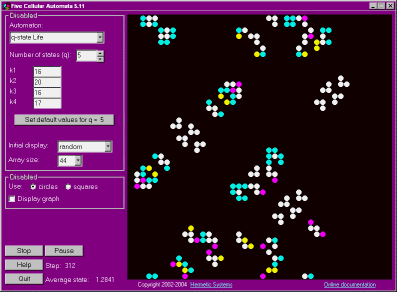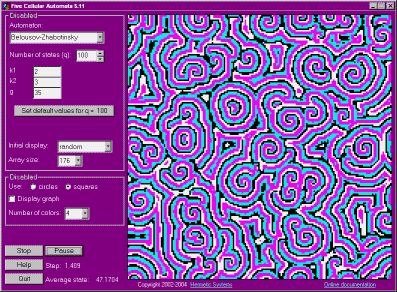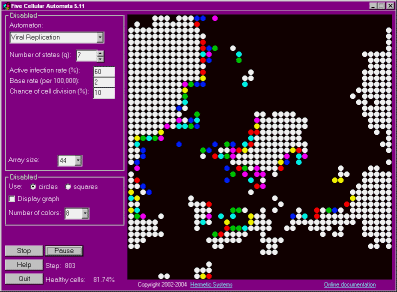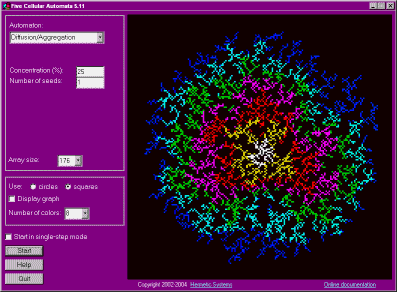
1. An extended version of Conway's Life, called q-state Life.
2. A simulation of the Belousov-Zhabotinsky chemical reaction in which, beginning from a random state of the system, spirals and curlicues "spontaneously" emerge.
3. A process called Togetherness in which cells with random states move so as to maximize the number of neighbors of each cell in the same state as that cell (or, thought of in another way, in which the cells rearrange themselves so as to form maximal clusters of cells all having the same state).
4. Viral Replication, a simulation of a population of dividing cells subject to viral infection.
5. Diffusion-Limited Aggregation, illustrating a process in which particles diffuse (moving randomly) and aggregate to form a fractal structure.
An explanation of the workings of each of these cellular automaton, and how to explore them using the software, may be found by following the links above.
A more theoretical explanation
A cellular automaton consists of:
(a) A structure of cells, such as the squares on a chess board.
(b) A set of values or "states" such that each cell is associated with a particular state.
(c) A set of rules describing how one state of the system (a particular configuration of cells in specific states) is to be transformed or converted to another state of the system.
A simple and well-known example of a cellular automaton is John Conway's Life. In this we consider a square array of cells, each of which is either "dead" or "alive". The eight cells immediately adjacent to a cell are called its "neighbors". The rules governing the dynamics of the system are as follows:
(i) In the transition from one "generation" to the next the state of each cell is changed once according to rules (ii) and (iii).
(ii) A cell which is alive will remain alive in the next
generation if there are two or three cells among its eight
neighbors which are alive; otherwise it dies.
(iii) A cell which is dead will remain dead in the next
generation unless there are exactly three cells among its
neighbors which are alive, in which case it becomes alive.
Five Cellular Automata allows exploration of five different cellular automata. All of them use a 2-dimensional array of cells which can vary in size from 33x33 to 528x528. "Periodic boundary conditions" are used, meaning that the left edge of the array wraps around to contact the right edge, and the top edge of the array wraps around to contact the bottom edge. The structure is thus that of a torus, although it is easier to think of a 2-dimensional plane in which an unlimited number of copies of the square array are reproduced next to, and above and below, each other (and each copy changes in the same way).
In each of these five automata the number of states is q (so that each cell is always in one of the states 1, 2, ..., q). The range of q depends on the automaton.
Saving Images
An image from any of the automata at any step may be saved to a .bmp file (817KB in size). After starting a run, and when the process is stopped or paused, a right-mouse-click (when the cursor is over the display) will bring up a dialog box asking if you wish to save the image. If so you can select the name and location for the .bmp file in which the image is to be saved: