---

1. Preamble

The fixed 7-day week is so much a part of daily life that it is commonly assumed to be as old as human society. However, this is not the case. In fact the fixed 7-day week was not widely used until it was introduced into the Julian Calendar in the 4th Century CE by the Emperor Constantine. Previously it was used by Jews and by early Christians, who had received it from the Jews, who had received a command that one day of every seven be allowed for rest, the other six days being for work.¹

Apart from this tradition of six days of work and one of recuperation there is no basis for using seven days as a unit of time except by association with seven objects of some kind. It has been suggested that the 7-day week arose by association of days with the Sun, the Moon and the five visible planets. Be that as it may, we now know that there are (at least) eight planets in our solar system other than the Earth, all of which are visible with or without the use of a simple telescope, so we can no longer justify a week of seven days by reference to the number of visible planets.

Although some forms of life exhibit cycles of 29-30 days (influenced by the Moon) there is no naturally occurring cycle of seven days. In human society at present this cycle runs on continuously but it has no harmonious relation with the other units of time, the month and the year. The 7-day week exists solely because of social habit and religious tradition, with otherwise no justification.

---

After the day, the next natural period of time is three days: a day of preparation followed by a day of active or passive participation followed by a day of rest and reflection. Thus the triday, a period of three successive days, is the next unit of time longer than a day which naturally accords with patterns of human activity.

If the first of two tridays is characterized by some condition, e.g., of work, and the second by some contrasting condition, e.g., of relaxation or of recreation, then a succession of pairs of such tridays consitutes a rhythmic process, e.g., work followed by recreation followed by work and so on:

The triday is thus the basis for a natural rhythm in life, in contrast to the 7-day week, which is an unnatural imposition.²

In the Liberalia Triday Calendar all units of time longer than a triday are composed of a whole number of tridays. Thus the calendar expresses a rhythmic flow of time in accord with a natural pattern of human activity.

---

2. Definition of the Calendar

The Liberalia Triday Calendar combines a solar calendar and a lunar calendar, which are independent but have tridays in common. One can use either or both according to one's preference or according to social requirements.

The units of time in the Liberalia Triday Calendar are:

• the day (in the sense of the nucthemeron, a day and a night, considered to run from midnight to midnight)
• the triday (a period of three consecutive days)
• the month (approximately a lunation)
• the quarter (a quarter-year)
• the lunar year
• the solar year
• the lunar year cycle and
• centuries and millennia of solar years.

The Solar Liberalia Triday Calendar designates days by means of dates of the form:

(solar) year

—

quarter

—

triday

—

day

The Lunar Liberalia Triday Calendar designates days by means of dates of the form:

cycle

—

(lunar) year

—

month

—

triday

—

day

Lunar dates are distinguished by "LLT" for "Lunar Liberalia Triday [Calendar]", and solar dates by "SLT" for "Solar Liberalia Triday [Calendar]".

The solar year number can be any integer, -2, -1, 0, 1, 2, 3, ...

A solar year consists of four quarters. In the Solar Liberalia Triday Calendar the quarter is designated either by name or by a number from 1 through 4.

The (lunar) cycle number can be any integer, -2, -1, 0, 1, 2, 3, ...

A (lunar) cycle always consists of 384 lunar years.³

A lunar year always consists of exactly twelve months. In the Lunar Liberalia Triday Calendar the month is identified either by name or as a number from 1 through 12.

The day is identified either by name or by a number from 1 through 3. Tridays succeed each other with no intervening days, and a triday in the lunar calendar always coincides with a triday in the solar calendar.

The rules for how many tridays are in a given quarter in a given solar year, and how many tridays are in a given month in a given lunar year, are given below.

Tridays in a quarter

The 1st and 3rd quarters always have 30 tridays. The 2nd quarter always has 31 tridays. The fourth quarter normally has 31 tridays but has 30 if the solar year number + 1 is divisible by 4 or by 198.⁴ In other words:

The 1st and 3rd quarters have 30 tridays (90 days) each.

The 2nd quarter has 31 tridays (93 days), and the 4th quarter has

31 tridays (93 days) unless the solar year + 1 is divisible by 4 or by 198,

in which case it has 30 tridays (90 days).

Tridays in a month

The first eleven months of each lunar year each have a constant number of months; they all have 10 tridays except that the 6th month has 9 tridays. The 12th month has either 9 or 10 tridays. It has 9 tridays unless the lunar year number minus 2 is divisible by 8, in which case it has 10 tridays, unless the lunar year number is 2, in which case it has 9 tridays. In other words:

Months 1 through 5, and 7 through 11, have 10 tridays (30 days) each.
Month 6 has 9 tridays (27 days), and month 12 has
9 tridays (27 days)	if the lunar year is 2, otherwise it has
10 tridays (30 days)	if the lunar year - 2 is divisible by 8, otherwise it has
9 tridays (27 days)

A century consists of 100 solar years, and a millennium consists of 1000 solar years. For years 0 and onward centuries and millennia begin with '00 years; centuries end with '99 years and millennia end with '999 years.

This completes the definition of the structure of the Liberalia Triday Calendar. The names for the days, the months and the quarters are given in the next section. The situation of the calendar in empirical time will be done in Section 6 below.

---

3. Names of the Days, Months and Quarters

The days in each triday are named:

1		2		3
Sophiesday		Zoesday		Norasday

The quarters of the solar year are named:

Quarter number	Quarter    name	Number    of tridays
1	Kamaliel	30
2	Gabriel	31
3	Samlo	30
4	Abrasax	30 or 31

The months in the lunar year are named:

Month number	Month    name	Number    of tridays		Month number	Month    name	Number    of tridays
1	Armedon	10		7	Mellephaneus	10
2	Nousanios	10		8	Loios	10
3	Harmozel	10		9	Davithe	10
4	Phaionios	10		10	Mousanios	10
5	Ainios	10		11	Amethes	10
6	Oraiel	9		12	Eleleth	9 or 10

---

4. The Calendar in Tabular Form

Here is the structure of the Liberalia Triday Calendar in tabular form, one table for the solar calendar and one table for the lunar calendar. These tables are also in SLTC.HTM and in LLTC.HTM for easy printing.

The Solar Liberalia Triday Calendar⁵

Kamaliel Triday Days 1 1 2 3 2 1 2 3 3 1 2 3 4 1 2 3 5 1 2 3 6 1 2 3 7 1 2 3 8 1 2 3 9 1 2 3 10 1 2 3 11 1 2 3 12 1 2 3 13 1 2 3 14 1 2 3 15 1 2 3 16 1 2 3 17 1 2 3 18 1 2 3 19 1 2 3 20 1 2 3 21 1 2 3 22 1 2 3 23 1 2 3 24 1 2 3 25 1 2 3 26 1 2 3 27 1 2 3 28 1 2 3 29 1 2 3 30 1 2 3		Gabriel Triday Days 1 1 2 3 2 1 2 3 3 1 2 3 4 1 2 3 5 1 2 3 6 1 2 3 7 1 2 3 8 1 2 3 9 1 2 3 10 1 2 3 11 1 2 3 12 1 2 3 13 1 2 3 14 1 2 3 15 1 2 3 16 1 2 3 17 1 2 3 18 1 2 3 19 1 2 3 20 1 2 3 21 1 2 3 22 1 2 3 23 1 2 3 24 1 2 3 25 1 2 3 26 1 2 3 27 1 2 3 28 1 2 3 29 1 2 3 30 1 2 3 31 1 2 3		Samlo Triday Days 1 1 2 3 2 1 2 3 3 1 2 3 4 1 2 3 5 1 2 3 6 1 2 3 7 1 2 3 8 1 2 3 9 1 2 3 10 1 2 3 11 1 2 3 12 1 2 3 13 1 2 3 14 1 2 3 15 1 2 3 16 1 2 3 17 1 2 3 18 1 2 3 19 1 2 3 20 1 2 3 21 1 2 3 22 1 2 3 23 1 2 3 24 1 2 3 25 1 2 3 26 1 2 3 27 1 2 3 28 1 2 3 29 1 2 3 30 1 2 3		Abrasax Triday Days 1 1 2 3 2 1 2 3 3 1 2 3 4 1 2 3 5 1 2 3 6 1 2 3 7 1 2 3 8 1 2 3 9 1 2 3 10 1 2 3 11 1 2 3 12 1 2 3 13 1 2 3 14 1 2 3 15 1 2 3 16 1 2 3 17 1 2 3 18 1 2 3 19 1 2 3 20 1 2 3 21 1 2 3 22 1 2 3 23 1 2 3 24 1 2 3 25 1 2 3 26 1 2 3 27 1 2 3 28 1 2 3 29 1 2 3 30 1 2 3 31 1 2 3
1 2 3 31st triday of Abrasax is omitted if year number + 1 is divisible by 4 or by 198

---

The Lunar Liberalia Triday Calendar

1 Armedon Tri. Days 1 1 2 3 2 1 2 3 3 1 2 3 4 1 2 3 5 1 2 3 6 1 2 3 7 1 2 3 8 1 2 3 9 1 2 3 10 1 2 3

2 Nousanios Tri. Days 1 1 2 3 2 1 2 3 3 1 2 3 4 1 2 3 5 1 2 3 6 1 2 3 7 1 2 3 8 1 2 3 9 1 2 3 10 1 2 3

3 Harmozel Tri. Days 1 1 2 3 2 1 2 3 3 1 2 3 4 1 2 3 5 1 2 3 6 1 2 3 7 1 2 3 8 1 2 3 9 1 2 3 10 1 2 3

4 Phaionios Tri. Days 1 1 2 3 2 1 2 3 3 1 2 3 4 1 2 3 5 1 2 3 6 1 2 3 7 1 2 3 8 1 2 3 9 1 2 3 10 1 2 3

5 Ainios Tri. Days 1 1 2 3 2 1 2 3 3 1 2 3 4 1 2 3 5 1 2 3 6 1 2 3 7 1 2 3 8 1 2 3 9 1 2 3 10 1 2 3

6 Oraiel Tri. Days 1 1 2 3 2 1 2 3 3 1 2 3 4 1 2 3 5 1 2 3 6 1 2 3 7 1 2 3 8 1 2 3 9 1 2 3

7 Mellephaneus Tri. Days 1 1 2 3 2 1 2 3 3 1 2 3 4 1 2 3 5 1 2 3 6 1 2 3 7 1 2 3 8 1 2 3 9 1 2 3 10 1 2 3	8 Loios Tri. Days 1 1 2 3 2 1 2 3 3 1 2 3 4 1 2 3 5 1 2 3 6 1 2 3 7 1 2 3 8 1 2 3 9 1 2 3 10 1 2 3	9 Davithe Tri. Days 1 1 2 3 2 1 2 3 3 1 2 3 4 1 2 3 5 1 2 3 6 1 2 3 7 1 2 3 8 1 2 3 9 1 2 3 10 1 2 3	10 Mousanios Tri. Days 1 1 2 3 2 1 2 3 3 1 2 3 4 1 2 3 5 1 2 3 6 1 2 3 7 1 2 3 8 1 2 3 9 1 2 3 10 1 2 3	11 Amethes Tri. Days 1 1 2 3 2 1 2 3 3 1 2 3 4 1 2 3 5 1 2 3 6 1 2 3 7 1 2 3 8 1 2 3 9 1 2 3 10 1 2 3	12 Eleleth Tri. Days 1 1 2 3 2 1 2 3 3 1 2 3 4 1 2 3 5 1 2 3 6 1 2 3 7 1 2 3 8 1 2 3 9 1 2 3 10 1 2 3
1 2 3 10th triday of Eleleth is included only if year is not 2 and year-2 is divisible by 8

---

5. Properties of the Calendar

1. The average length of the solar year

From the rule for the number of tridays in each quarter of a solar year we may conclude that in 396 (=2*198) successive solar years there are:

• 396*(30+31+30) tridays in the non-4th quarters of all years
• 2*30 tridays in the 4th quarters of the two years whose year number + 1 is divisible by 198
• (396/4 - 1)*30 tridays in the 4th quarters of other years whose year number + 1 is divisible by 4
• (396 - (396/4 - 1) - 2)*31 tridays in the 4th quarters of the other years.

Thus the total number of tridays in 396 solar years is 36,036 + 60 + 2,940 + 9,176 = 48,212, and so the total number of days in 396 solar years is 144,636.

Thus the average length of a solar year is 144,636/396 = 12,053/33 = 365.2424 days (to four decimal places). This is the same as the current length of the vernal equinox year.

2. The average length of the lunar year

From the rule for the number of tridays in a month we may conclude that in one cycle of 384 successive lunar years there are:

• 384*(10*10 + 9) tridays in the non-12th months of all years
• 9 tridays in the 12th month of the year whose year number is 2
• (384/8 - 1)*10 tridays in the 12th months of other years whose year number minus 2 is divisible by 8
• (384 - (384/8 - 1) - 1)*9 tridays in the 12th months of the other years

Thus the total number of tridays in one cycle of 384 lunar years is 41,856 + 9 + 470 + 3,024 = 45,359, so the total number of days in one cycle is 136,077.

The structure of the lunar calendar repeats with each cycle of 384 lunar years. Thus the average length of a lunar year is 136,077/384 = 45,359/128 = 354.3672 days (to four decimal places).

3. The average length of the month

We have just seen that there are 136,077 days in one cycle of 384 lunar years. Each lunar year has exactly 12 months so in 384 lunar years there are 4,608 months. Thus the average length of a month is 136,077/4,608 = 45,359/1,536 = 29.530599 days (to six decimal places).

The observed synodic month is currently 29.530589 days in length, on average, and is decreasing (it is expected to reach about 29.530583 days by the year 3000 CE). Thus the average month length in the Liberalia Triday Calendar is slightly more than the current synodic month. However, even assuming the lower 3000 CE value of the synodic month, if the synodic month were to remain constant at this value the number of months before the average beginnings of the synodic month and the calendar month would diverge by about a day is 1/( 29.530599 - 29.530583 ) = 62,500 months. This is (62,500*29.530599) / 365.2424 = 5,053 vernal equinox years, so on average the months of this calendar will, on average, remain in sync with the lunar cycles for some millennia yet.

4. The cycle length of the calendar

The "cycle length" of a rule-based calendar is the smallest number of days which contains the "complete structure" of the calendar. For example, the cycle length of the Julian Calendar is 3*365 + 366 = 1461 days, and the structure of three 365-day years and one 366-day year repeats itself every four Julian years.

Because of the leap-year rule of the Gregorian calendar its cycle length is 366 + 3*365 + 96*366 + 300*365 = 146,097 days, or 400 Gregorian years.

What is the cycle length of the Liberalia Triday Calendar? This calendar combines two cycles, a solar calendar cycle and a lunar calendar cycle. We have seen above that the length of the solar calendar cycle is 144,636 days and that of the lunar calendar cycle is 136,077 days. The smallest period of time which contains multiples of each of these cycles is the least common multiple of their lengths. The prime decompositions of these two cycle lengths are, respectively, 2²*3*17*709 and 3*67*677. The l.c.m. is 2²*3*17*67*677*709 = 6,560,544,324 days. Thus the cycle length of the Liberalia Triday Calendar is 17,962,164 solar years.

5. The triday offset

There is a relationship between the triday numbers in lunar and solar calendar dates which allows us to infer the value of the triday number in a lunar date if the triday number of the corresponding solar date is known, provided we know the current triday offset.⁶

The "triday offset", for a particular triday, is the number required to be added to the triday of the solar date to produce the number which is equal modulus 10 to the triday of the lunar date.

For example, consider a date such as "Zoesday, 5 Loios 98, 21 Samlo 95" ( 98-08-05-2 LLT / 95-3-21-2 SLT ). Here the solar triday number is 21. In this case the triday offset is 4, because by adding 4 to 21 we obtain 25, which is equivalent modulo 10 to 5, the lunar triday number.⁷

The triday offset changes only a few times in a year. In fact, it changes only when a new solar or lunar half-year begins. A solar half-year begins on the 1st day of the 1st or the 3rd quarter. A lunar half-year begins on the 1st day of the 1st or the 7th month. If we designate the current value of the triday offset by OFF the rule for when the triday offset changes (and how it changes) can be formulated as follows:⁸

1. If today is not the beginning of a lunar half-year or a solar half-year then OFF has the same value as yesterday.
2. If today is both the beginning of a lunar half-year and is the beginning of a solar half-year then OFF = 0.
3. If today is a solar new year and the year number is divisible by 4 or by 198 then OFF is unchanged.
4. If today is a lunar new year and the year number is not 3 and year-3 is divisible by 8 then OFF is unchanged.
5. Otherwise if OFF is 9 then OFF becomes 0, otherwise add 1 to OFF.

---

6. Correlation with Empirical Time

The use in practice of any calendar requires that a particular date in the calendar be identified with a particular day in the sequence of days that have been experienced on Earth (or on whatever planet it is intended for). The Julian day number system is often used to specify particular days, and we so use it here.

The lunar date 0-000-01-01-1 LLT is a short way of referring to Sophiesday in the first triday in the month Armedon in the lunar year 0 in cycle 0. The solar date 0-1-01-1 SLT means Sophiesday in the first triday in the quarter Kamaliel in the solar year 0.

These two dates designate the same day, namely the day whose Julian day number is 2,416,557. In the Common Era Calendar this day is 1904-03-17, or March 17th in the year 1904 CE.

That day was distinguished by a central annular eclipse, which occurred at 5:40 UTC. Somewhat less than four days later the vernal equinox occurred on 1904-03-21 CE at 1:01 UTC.

This correlation of the first day of lunar year 0 (in cycle 0) and the first day of solar year 0 with a particular day, identified by its Julian day number, allows us to construct a one-to-one correspondence between lunar and solar dates in the Liberalia Triday Calendar, Julian day numbers and dates in the Common Era Calendar. Thus:

      JDN         CE date           lunar date         solar date
    2416554      1904-03-14     -1-383-12-09-1 LLT    -1-4-30-1 SLT
    2416555      1904-03-15     -1-383-12-09-2 LLT    -1-4-30-2 SLT
    2416556      1904-03-16     -1-383-12-09-3 LLT    -1-4-30-3 SLT
    2416557      1904-03-17      0-000-01-01-1 LLT     0-1-01-1 SLT
    2416558      1904-03-18      0-000-01-01-2 LLT     0-1-01-2 SLT
    2416559      1904-03-19      0-000-01-01-3 LLT     0-1-01-3 SLT
    2416560      1904-03-20      0-000-01-02-1 LLT     0-1-02-1 SLT
    2416561      1904-03-21      0-000-01-02-2 LLT     0-1-02-2 SLT
    2416562      1904-03-22      0-000-01-02-3 LLT     0-1-02-3 SLT
    2416563      1904-03-23      0-000-01-03-1 LLT     0-1-03-1 SLT
    2416564      1904-03-24      0-000-01-03-2 LLT     0-1-03-2 SLT
    2416565      1904-03-25      0-000-01-03-3 LLT     0-1-03-3 SLT

For dates in cycle 0 we may omit the cycle number, so a lunar date of the form year-month-triday-day (with no cycle number) is to be understood as 0-year-month-triday-day (where the possible year numbers are 0 through 383). Thus, e.g., 0-000-01-03-3 LLT is the same as 0-01-03-3 LLT.

Further correspondences are given in LTCDATES.HTM.

The solar new year's days for the next 16 years are as follows:

      JDN          CE date         lunar date         solar date
    2451621      2000-03-17      098-12-05-1 LLT    96-1-01-1 SLT
    2451987      2001-03-18      099-12-08-1 LLT    97-1-01-1 SLT
    2452353      2002-03-19      101-01-03-1 LLT    98-1-01-1 SLT
    2452719      2003-03-20      102-01-07-1 LLT    99-1-01-1 SLT
    2453082      2004-03-17      103-01-10-1 LLT   100-1-01-1 SLT
    2453448      2005-03-18      104-02-04-1 LLT   101-1-01-1 SLT
    2453814      2006-03-19      105-02-08-1 LLT   102-1-01-1 SLT
    2454180      2007-03-20      106-03-02-1 LLT   103-1-01-1 SLT
    2454543      2008-03-17      107-03-04-1 LLT   104-1-01-1 SLT
    2454909      2009-03-18      108-03-08-1 LLT   105-1-01-1 SLT
    2455275      2010-03-19      109-04-02-1 LLT   106-1-01-1 SLT
    2455641      2011-03-20      110-04-06-1 LLT   107-1-01-1 SLT
    2456004      2012-03-17      111-04-09-1 LLT   108-1-01-1 SLT
    2456370      2013-03-18      112-05-03-1 LLT   109-1-01-1 SLT
    2456736      2014-03-19      113-05-07-1 LLT   110-1-01-1 SLT
    2457102      2015-03-20      114-06-01-1 LLT   111-1-01-1 SLT

A day may be identified either by its solar date or by its lunar date, so for purposes of identification only one of these is needed.

The combined form, as in "Norasday, 9 Davithe 98, 5 Abrasax 95" (corresponding to 98-09-09-3 LLT / 95-4-05-3 SLT), is like stating a date in both a sacred and a civil calendar, e.g., 6 Chicchan 13 Zac in the Maya Calendar.

Conversion between dates in the Liberalia Triday Calendar and dates in the Common Era Calendar can be performed by means of the Lunar Calendars and Eclipse Finder software.

---

7. Variation of the Vernal Equinox

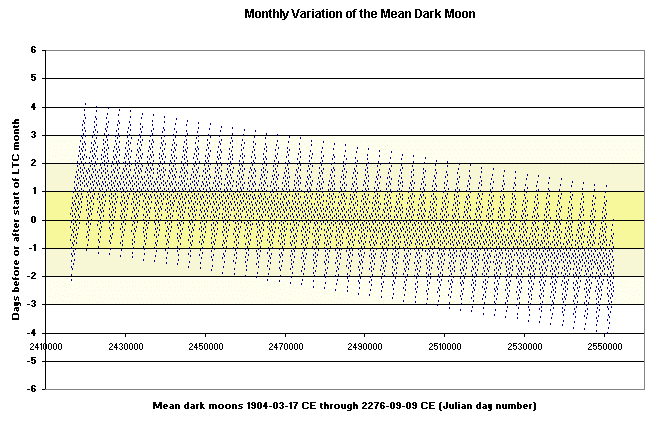
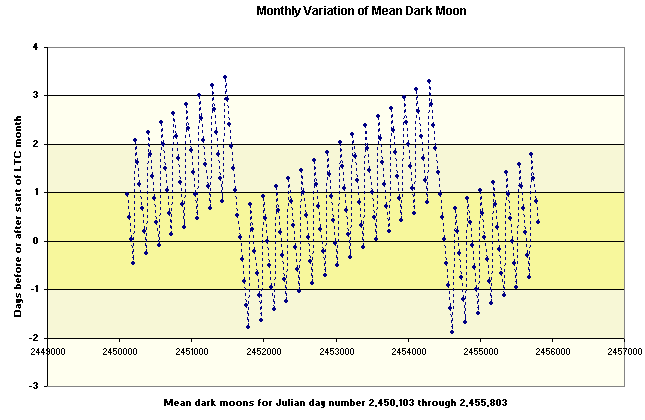
A solar calendar accords with the seasons, with each year in the calendar corresponding to one revolution of the Earth about the Sun. With respect to a solar calendar the equinoxes and the solstices should occur at approximately the same date each year. In all solar calendars which are rule-based there is some variation of the vernal equinox date. Even in the Gregorian Calendar, which aims to keep the vernal equinox on a single date, there is a variation of about 53 hours (with the effect that the vernal equinox can occur on any of March 19, 20 and 21).

In any rule-based calendar there is a trade-off between, on the one hand, the simplicity of the rules defining the number of days in a month and in a year, and on the other, the precision with which some target astronomical phenomenon (such as the vernal equinox or the full moon) can be tracked. It is difficult (if not impossible) to create a rule-based solar calendar with simple rules which keeps the vernal equinox on some constant day in the calendar year, and it seems quite impossible to create a rule-based lunar calendar which keeps the dark moon (or the full moon) on some constant day in the calendar month (at least without using extremely complex rules)

The Liberalia Triday Calendar has rules which are fairly simple (and which are thus easy to remember). Nothing more than elementary arithmetic is required to determine the number of days in a month, a quarter or a year. Thus some significant degree of variation is to be expected when it comes to tracking the vernal equinox and the dark and full moon.

---

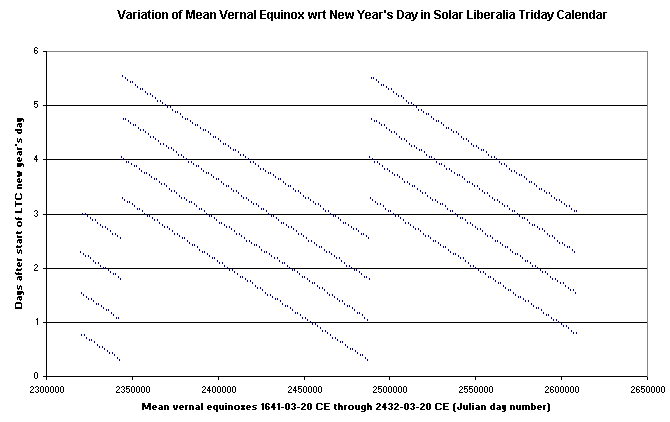
The date of the vernal equinox in 1641 CE was March 20 (JDN 2,320,502); it occurred at 7:03 UTC. The length of the vernal equinox year is 365.2424 days. By adding 365.2424 days 396 times to the date and time of this vernal equinox we may obtain dates (and times) in the solar year of the Liberalia Triday Calendar of the "mean vernal equinox" over an entire solar cycle of 396 solar years. Because there is little variation over a period of several hundred years in the length of the vernal equinox year (as distinct from the variation in the date of the vernal equinox in the Common Era Calendar) this will give a fairly accurate estimate of how the vernal equinox varies with respect to the Solar Liberalia Triday Calendar.

The results of this study are shown in the following plot, which shows the number of days after the beginning of new year's day in the solar calendar for the occurrence of the mean vernal equinox, plotted over the period 1641-03-20 CE through 2432-03-20 CE (a period of 4*198 = 2*396 = 792 years):

This study shows that over a 396-solar-year period the vernal equinox ranges from a maximum of 5.54 days (133 hours) after midnight at the start of new year's day in the solar calendar to a minimum of 0.29 days (7 hours) after midnight. This pattern repeats itself every 396 solar years.

Thus we can conclude that in the Solar Liberalia Triday Calendar the vernal equinox always occurs in one of the first two tridays of the first quarter of the solar year. In the years following 2000 CE the vernal equinox will vary in cycles of four years from about 3.3 days ahead of the beginning of solar new year's day to about 0.9 days ahead, becoming earlier in each phase of the cycle at about 0.75 days per century. The next earliest vernal equinox will be the one occurring at 7:19 UT on the solar new year's day of 195 (2099-03-20 CE).

---

8. Variation of the Dark Moon

A lunar calendar aims to have some particular phase of the Moon occur at approximately the same date in each calendar month. In the Liberalia Triday Calendar the phase at which the month begins is the dark moon (the conjunction of Moon and Sun).⁸

Having a calendar month in a lunar calendar begin at some particular phase of the Moon is trivially accomplished if the start of a month is determined by observation of the Moon. In all rule-based lunar calendars, on the other hand, there is usually a variation of several days in the calendar dates of the dark moon and the full moon.

The synodic month is 29.530589 days at present. This is the average time either from dark moon to dark moon, or from full moon to full moon. On average a full moon occurs 14.765 days after a dark moon, so in order to ascertain how well the Lunar Liberalia Calendar tracks the full moon it is sufficient to ascertain how well it tracks the dark moon.

As noted above, there was a solar eclipse (and thus a dark moon) on the first day of the first lunar year (of cycle 0), on 1904-03-17 CE (JDN 2,416,557) at 5:40 UTC. By adding 29.530589 days 384 times to the date and time of this dark moon we may obtain dates (and times) in the lunar year of the Liberalia Triday Calendar of the "mean dark moon" over an entire lunar cycle of 384 lunar years. Due to the dynamics of the Earth/Moon/Sun system there is a significant amount of variation in the length of a lunation, which can range from 29.27 days to 29.82 days. Thus the calculated time of a mean dark moon may differ from the time of the real dark moon by a significant amount. Nevertheless the variation of the mean dark moon does provide a reasonable estimate of how the dark moon varies with respect to the Lunar Liberalia Triday Calendar.

The results of this study are shown in the following plot, which shows the number of days before or after the beginning of the first day of the month in the lunar calendar for 4,608 mean dark moons, plotted over the period 1904-03-17 CE through 2276-09-09 CE:

This study shows that over a 384-lunar-year period the mean dark moon ranges from a maximum of 4.08 days (98 hours) after midnight at the start of the 1st day of the month in the lunar calendar to a maximum of 4.00 days (96 hours) before that start. The mean of these means is 16 hours after the start of the first day of the month. This pattern repeats itself every 384 lunar years.

The numbers and percentages of these 4608 mean dark moons falling less than +/- n days from the start of the first day are as follows:

1 day	2 days	3 days	4 days	5 days
2199	3753	4438	4605	4608
47.72%	81.45%	96.31%	99.93%	100.00%

Assuming that this result for the mean dark moon holds for the real dark moon we can expect that nearly half of the dark moons will occur either on the first or the last day of the month and that about 24 out of 25 dark moons will occur in either the first or the last triday of the month.

The following plot shows the occurrences of the mean dark moon with respect to the 1st of the month for the period January 1996 CE through August 2011 CE:

Since the dark moon always occurs in the first four days or the last four days of a month and the full moon always occurs close to fifteen days after the dark moon, it is reasonable to expect that the full moon will always occur no earlier than the 12th day of the month and no later than the 19th day, and that nearly half of the full moons will occur either on the 15th or the 16th day.

As is to be expected, there is no correlation between the dark moons and the tridays in the solar calendar. Dark moons occur fairly evenly in all tridays of the quarters (except for the 31st).

---

9. Advantages of the Calendar for Business

By "business" we mean here any organization involving more than one person cooperating in some ongoing activity. This includes not only businesses as usually understood but also government activities.

1. One of the standard objections to the Common Era Calendar is that dates have no regular association with days of the week. January 1st may be a Saturday in one year, but in the next year it will not be, and given a date it is far from obvious what day of the week it will occur on.

In the Liberalia Triday Calendar a given date in a year, whether lunar or solar, always has the same day name regardless of the year. For example, 111-04-07-3 LLT is Norasday, and the 3rd day of the 7th triday of the 4th month will always be Norasday regardless of the year. Similarly 110-3-28-2 SLT is Zoesday, and the 2nd day of the 28th triday of the 3rd quarter will always be Zoesday regardless of the year.

The first day of a triday, a month, a quarter, a lunar year or a solar year is always Sophiesday. The last day of a triday, a month, a quarter, a lunar year or a solar year is always Norasday.

2. Businesses often find the division of the year into quarters and months of unequal and irregular lengths to be a nuisance for bookkeeping and scheduling. For this purpose the division of the solar year into quarters, each of which has 30 or 31 tridays (i.e., 90 or 93 days) is useful.

3. Currently most business run for five days out of seven and shut down for two. This 2-day interruption is inconvenient and reduces efficiency. On Friday afternoon employees and the business overall are winding down at the end of the week, and they require most of Monday morning to start up again. So the business is either not running or is running at half-pace for ½ + 2 + ½ = 3 days out of 7.

Businesses would be more efficient if they never shut down. Since employees (and employers) need time to lead their own lives a solution is for the business to run continuously without a break but to have only half the personnel at work on any given day. The Liberalia Triday Calendar accords well with such an arrangment, as will now be shown.

The simplest work scheme is to have two teams of personnel who work on alternating tridays, as follows:

Triday	1			2			3			4
Day	1	2	3	1	2	3	1	2	3	1	2	3
Team 1	on			off			on			off
Team 2	off			on			off			on

This is OK for smaller organizations. For larger organizations it may be important that not all of the personnel begin or end their 3-day shift at the same time. In this case the following scheme may be preferable:

Triday

1

2

3

4

Day

1

2

3

1

2

3

1

2

3

1

2

3

Team 1

on

off

on

off

Team 2

off

on

off

on

off

Team 3

off

on

off

on

off

Team 4

off

on

off

on

Team 5

on

off

on

off

on

Team 6

on

off

on

off

on

In this scheme, on every day one of the three teams working consists of people on the 1st day of their 3-day shift, one consists of people on the 2nd day, and one consists of people on the 3rd day.

Either of these schemes allows the business to run every day, with no down time or half-days required for personnel to wind down or start up. Employees work only three days out of six (better than five out of seven as at present) but the business is more efficient because it is running constantly and not down for two or three days out of seven.

---

10. Anniversaries

Another benefit of the adoption of the Liberalia Triday Calendar is that everyone gets to celebrate two birthdays in any one solar year, namely, their birthday according to the lunar calendar and their birthday according to the solar calendar.

For example, the highly respected and esteemed chemist Albert Hofmann (1906-2008), the first person to synthesize LSD and to discover its psychospiritual use, was born on 1906-01-11 CE, which is 1-11-05-3 LLT and 1-4-09-3 SLT. Had he adopted the Liberalia Triday Calendar before the start of the new millennium (in the Common Era Calendar) he would have celebrated his 94th birthday according to the solar calendar on 95-4-09-3 SLT (2000-01-13 CE). Dr Hofmann would also have celebrated his 100th birthday in the lunar calendar on 101-11-05-3 LLT (2003-01-18 CE).

Clearly this duality applies to all anniversaries, which may be celebrated according to the solar calendar, the lunar calendar or both.

As a related example, consider the widely-celebrated "Bicycle Day", the anniversary of the day, April 19th, 1943, when Dr Hofmann embarked upon the first intentional expansion of consciousness induced by the material he had discovered.¹⁰ 1943-04-19 CE is Sophiesday, 6 Phaionios 40, 11 Kamaliel 39. The anniversary of Bicycle Day in the lunar calendar is thus Sophiesday 6 Phaionios and in the solar calendar is Sophiesday 11 Kamaliel.

---

11. The Name of the Calendar

The day chosen to link the Liberalia Triday Calendar to empirical time is, as noted above, March 17, 1904 CE. In the Roman Calendar the Festival of Liberalia was celebrated on XVI Kalendas Aprilis, which corresponds (by counting back 16 days from, and including, April 1st) to the 17th day of March.

At http://www.clubs.psu.edu/Aegsa/rome/mar16.htm we read (or used to read, since it is now gone):

This day [March 17th] is for special religious observance.

This day was sacred to Liber [Freedom], and on this day women would line the streets and sell fresh meal-cakes on small altars. Processions were made to chapels in various parts of the city. Effigies were placed in these chapels, later to be cast into the Tiber river during the festivals in May.

The Liberalia is considered to be the first real festival of the new sacral year. A primary theme of these celebrations is freedom (liber).

Freedom to the Romans had four embodiments:

1. Freedom from evil.
2. Freedom from burdens.
3. Freedom from care.
4. Freedom from youthful folly.

This is the seventeenth day of the Festival of Mars. The daily spectacle of the priests of Mars leaping and dancing through the streets of Rome would continue this day. In fact, the multiple processions going on throughout the day would have borne a resemblance to the multiple parades that go on throughout New Orleans during Mardi Gras.

The Liberalia Triday Calendar is dedicated to freedom of religion, freedom from religous persecution and freedom to pursue spiritual knowledge by any desired means, including the use of psychedelics.

Liberalia Triday Calendar Date Conversion Software
Top of Page	Calendar Studies	Home Page